|
Hosted by the courtesy of GitHub |
The stars ASAP



 Durée du voyage intersidéral  Résolutions de l'ONU en HTML  Bussard Ramjet 
 |
DWARF : dwarf2xml
 ELF : libelf examples  Code presentation : ctoohtml  |
|
Hosted by the courtesy of GitHub |
The stars ASAP



 Durée du voyage intersidéral  Résolutions de l'ONU en HTML  Bussard Ramjet 
 |
DWARF : dwarf2xml
 ELF : libelf examples  Code presentation : ctoohtml  |
Translation : Emmanuel Azencot Author : Emmanuel Azencot Creation : Fri May 2 16:13:44 CEST 2014 Update: Tue Nov 13 10:33:03 CET 2018
Other bussards ramjets motion |

|
Ideal Bussard Ramjet Motion |
The interstellar travel is still nowadays a pure theoretical game. Sending human to the nearest stars is beyond our technological reach. There are only very little solutions, even theoretical, that could do it. Here, then, it is only a matter of theory and calculations in ideal cases.
The bussard ramjet coined in its principle by Dr. Bussard [1] drag the scarce interstellar material to satisfy the propulsion energy needs. As no propulsion fuel is carried by the mobile, Tsiolkovsky constraint [2] does not apply.
The constraint makes all known fuels including hydrogen nuclear fusion unable to reach required speed. The only fuels that are efficient enough are those who are almost fully converted into useful impulse. Some speculative theoretical solution have been proposed, including antimatter [3] or micro black holes [4].
Most studies on this device have shown that it is not the easiest way to the nearby stars and a working implementation, if it ever happen, will probably be after fuel caring vessels [5].
Indeed, the fascinating point is, for now, that it is not subject the Tsiolkovsky constraint. For this reason, it should later be used it to reach farther targets, as bussard ramjet does not seems to have terminal velocity other than speed of light [6].
In the following we will study the ideal case where all captured material and energy are converted optimally without any losses into impulse for the propulsion. This assumption leads to a case simple enough to allow a full and exact algebraic resolution of motion equations. An other interesting point about this case is that it is the most efficient Bussard Ramjet device.
I cannot guarantee the exactness of the following as this document have never be reviewed and so there should be several errors lying in. For this reason it would be very unwise of you to take it for correct. So I am very interested in any feedback you may send through email you will easily find on the site.
This very theoretical device converts the whole energy collected, mass and kinetic energy, into light emitted exactly in the axis of mobile. We will work in the comoving frame, instantaneously at rest relative to the device, as explained in "Short course in special relativity" [7].
We are going to use the conservation of energy and impulse summarized in special relativity formalism by 4-momentum. We scope 4-momentum at the begining of an infinitesimal interval of proper time τ and at τ+dτ, corresponding to interval t to t +dτ in medium frame.
|
|
c | is the speed of light. |
|
|
|
ρ | is the medium density. |
|
|
|
S | is the collection cross section |
|
|
|
M | is the weight of the rocket |
|
|
|
β | is speed of the rocket relative to the speed of light, v/c, in medium frame. |
|
|
|
η(x) | is the boost corresponding to the speed x. It is arctanh(x), inverse hyperbolic tangent. Unlike speed, boost is additive, and thus integrable. |
|
|
|
m | is the mass of the collected material. |
|
|
|
t | is a time stamp in the medium (or collected material) frame. |
|
|
|
τ | is a time stamp in the rocket frame. |
|
|
|
γ(x) | is the Lorentz factor suitable for two frames moving with speed x from each other. Its value is (1- x2)-1/2. |
|
|
|
γ | is the Lorentz factor corresponding to the speed β. |
|
|
|
Λ(x) | is the Lorentz transform matrix for the speed x, C.f (1.1). |
|
|
|
Β | Reduced and relative cross section for material collection, equal to ρSc / M. |
|
Between these to instants the rocket dredge an area S in a medium of density ρ. As it move forward of infinitesimal distance dx, it sweep a volume S dx during proper time dτ. We start working with spacetime event 4-vector proper time interval (c(τ +dτ), 0, 0, 0) and (cτ, 0, 0, 0) which can be simplified to ((c(τ +dτ), 0) -(cτ, 0,)), as only the dimension of space along motion is to be taken into account. We will use this simplification in the following.
We want the rocket proper time interval corresponding to (c dτ, 0) in the medium rest frame. According to special relativity, Lorentz transform matrix Λ(β) is the right way when the frames are moving from each other with speed β :
| (1.1) |
|
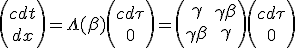
|
| (1.2) |
|
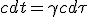
|
| (1.3) |
|
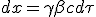
|
From (1.3) the device covered a distance dx, and then it sweep a volume S dx in which all the material, at density ρ, is collected : m = ρSdx. We just have to replace dx with (1.3) to have an expression of collected material as a function of time interval :
| (1.4) |
|
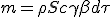
|
The rocket with mass M have a 4-vector momentum expressed in its own frame of :
|
|
|
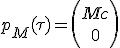
|
In order to have the momentum of collected interstellar gas we express it in the medium frame and then we change to the rocket frame which have a velocity of -β :
|
|
|
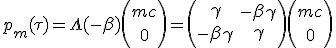
|
|
|
|
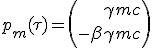
|
The 4-vector momentum of the system is the sum of the two previous contributions :
| (1.5) |
|
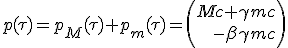
|
All collected mater m, including its kinetic energy, is converted into mass-less particles send toward x axis. Momentum of mass-less resulting beam is (q, -q) (1).
|
|
|
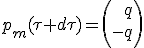
|
As we will see later, it useless to explicit q, although it is straightforward.
During time interval device speed increase by infinitesimal increment dβ, which give it the new momentum :
|
|
|
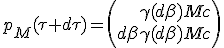
|
As speed increase dβ is as small as required, we can approximate its Lorentz factor γ(dβ) as being very close from 1. Indeed, at scale of dβ, a second order Tailor development of γ(dβ) give classical mechanic equivalent γ(dβ) ≈ 1 + ½ dβ2. As it is a second order of vanishing quantity, we can drop its contribution :
|
|
|
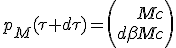
|
The new system momentum 4-vector at proper time τ +dτ is the sum of its contributors :
| (1.6) |
|
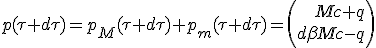
|
(1) A property of mass-less particles is the null self inner product of their momentum. As the momentum is a Lorentz transform invariant, and is m2c2.
The invariance of momentum 4-vector account for both impulse and energy conservation :
|
|
|
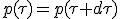
|
We now split time and space dimension into separate equations :
| (E) |
|
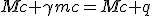
|
| (P) |
|
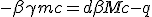
|
Having still collected material expression at (1.4) :
| (M) |
|
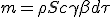
|
Adding (E) with (P), then using (M), and with :
| (1.7) |
|
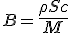
|
It comes :
|
|
|
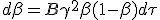
|
| (1.8) |
|
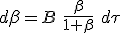 |
The graph below is Bβ / (1 + β), at sampled values of B 1, 0.1 and 10 (2). Only part where β ≥ 0 is to be considered.
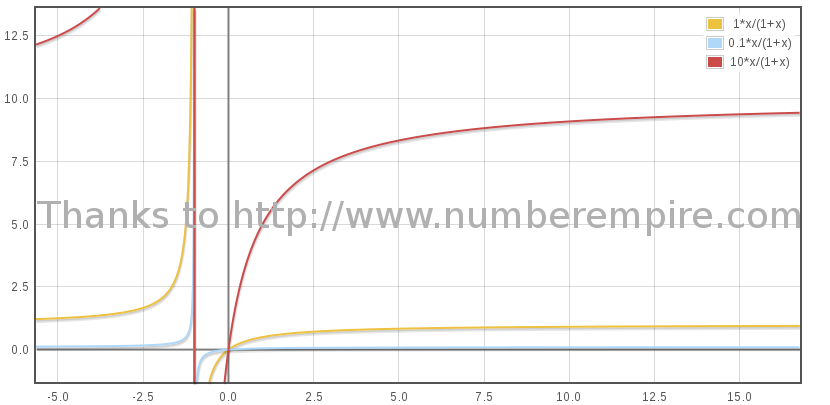
(2) The physical value of B is indeed very small as the particles in the medium are scarce, less than 0.1 proton/cm3 and as the rocket weight is a matter of thousand of tons.
Looking for an expression of β(τ), we want to integrate the previous differential equation. At first we try to figure the initial condition.
When β > 0, acceleration is positive, and hence β(τ) is increasing function of proper time τ as soon as β > 0. Moreover if β = 0, acceleration will also be null. It is then required an infinite amount of time for the device to get an non null speed. The initial condition based on β = 0, will be reach as time tend to -∞.
An other issue towards integration coming from β not being additive, is flattened by a variable substitution from β to boost, η(β) = η = atanh(β), which is additive. As the derivative of tanh(x) at x = 0 is 1, we can simply replace dβ with dη. The reworked equation (1.8) become :
|
|
|
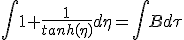
|
|
|
|
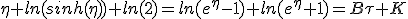 (3) (3) |
Fed in this result, initial condition constraint does no lead to any particular specific value of K, as any of its value is suitable for boost η going to zero as time τ goes to -∞. We then can choice K = 0 for simplify :
|
|
|
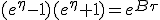
|
|
|
|
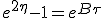
|
| (1.9) |
|
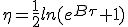
|
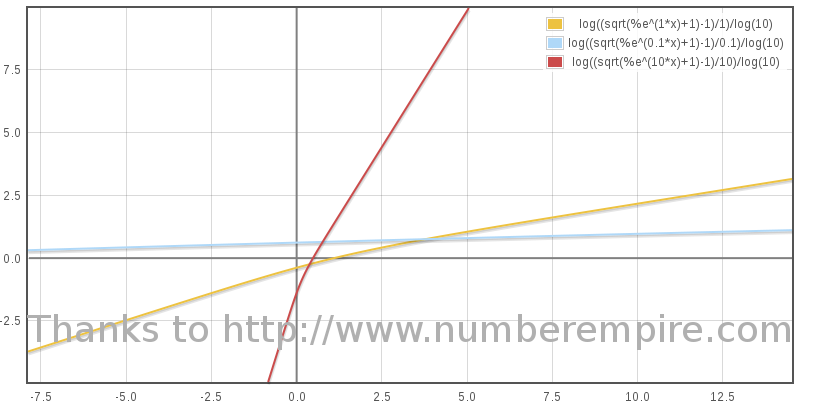
For τ = 0, 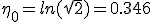 .
Converting boost back to β, we find
.
Converting boost back to β, we find 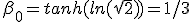 .
It follows that all the speed curves for any value of B cross at 1/3 of light speed. This crossing happen at τ = 0.
.
It follows that all the speed curves for any value of B cross at 1/3 of light speed. This crossing happen at τ = 0.
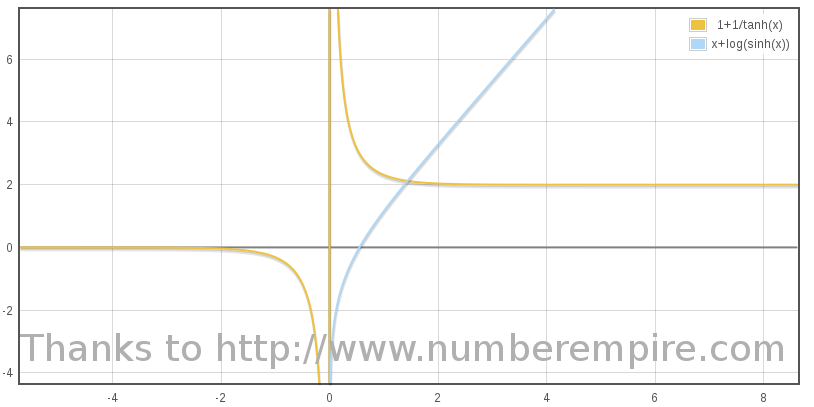
Below the graph of η(τ) for a some value of B : 1, 0.1 and 10 :
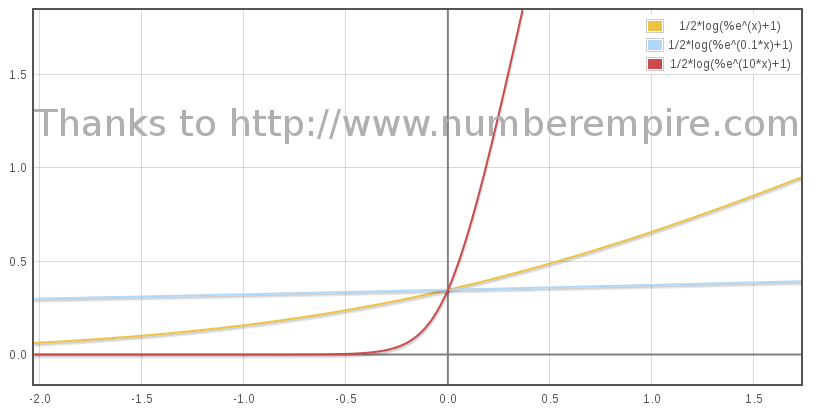
Its is straightforward to derive an expression of β as a function of τ using β = tanh(η) :
|
|
|
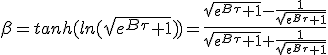
|
| (1.10) |
|
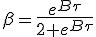
|
An approximate low speed expression, when τ tend to -∞ is an exponential motion,
|
|
|
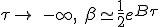
|
At high speed, when τ tend to +∞ as obtain from η lead to an approximate motion :
|
|
|
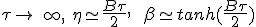
|
Below graph show evolution of β as a proper time function plotted for 3 values of B :
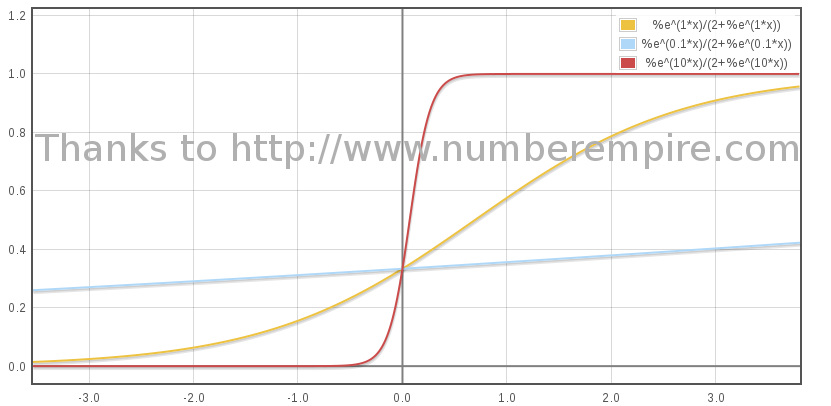
(3) Thanks to Mathématica for the first form and to NumberEmpire for the second.
We now focus on the distance traveled by the rocket in the medium frame. When accounting for medium collected matter, we found, according to (1.3) an expression of dx as a function of dτ. Remembering that γ = cosh(η) and βγ = sinh(η) :
|
|
|
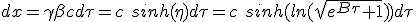
|
|
|
|
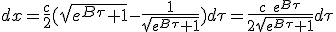
|
|
|
|
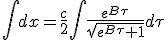
|
|
|
|
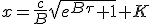
|
When τ goes to -∞, x must tend to 0. This constraint B to be -c/B, hence :
| (1.11) |
|
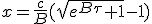
|
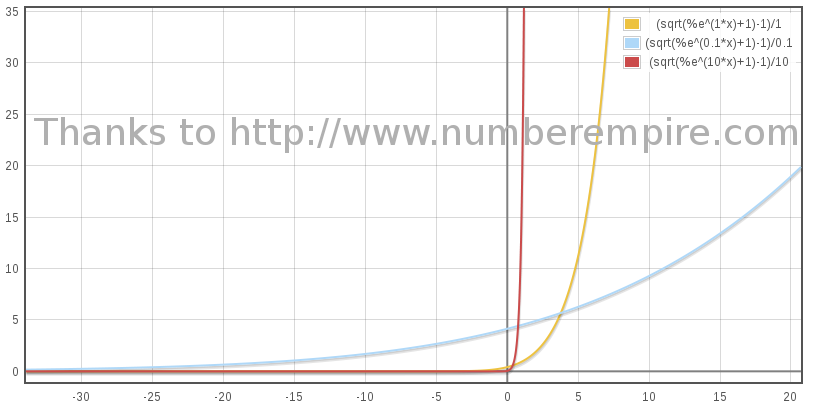
An enhanced view with the logarithm of x :
We can derive the distance traveled by the device at proper time τ = 0 :
| (1.12) |
|
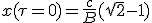
|
A traveler to Andromeda Galaxy will see Milky way spinning.
We are looking for how much time t that elapses in medium frame firstly as a function of rocket proper time τ. We start using (1.2) which join the corresponding infinitesimal quantities. Given boost expression from η at (1.9) :
|
|
|
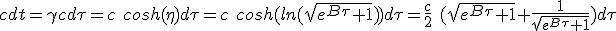
|
|
|
|
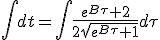
|
Thanks to Number Empire :
|
|
|
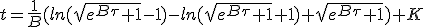
|
Having t = 0 when τ = 0, require
|
|
|
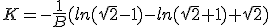
|
|
|
|
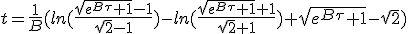
|
| (1.13) |
|
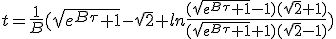
|
Clearly fixed frame do not make any sense as for special relativity. It is rather the frame of the collected matter, the medium frame, if indeed this material was having an homogenous motion. The "fixed" medium frame, can also be approximate with sun's proper frame neglecting the collected matter speed relative to it.
The value of x of (1.11) and t from (1.13) are then stated to be time and distance observed from Earth. In the case of ideal bussard ramjet it is possible to derive an algebraic exact expression of elapsed time as a function of traveled distance.
|
|
|
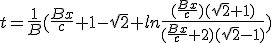
|
|
|
|
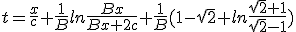
|
| (1.14) |
|
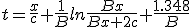
|
The following graph show the travel duration as a function of time that is t(x). Of course only the right part where x ≥ 0 is to be considered.
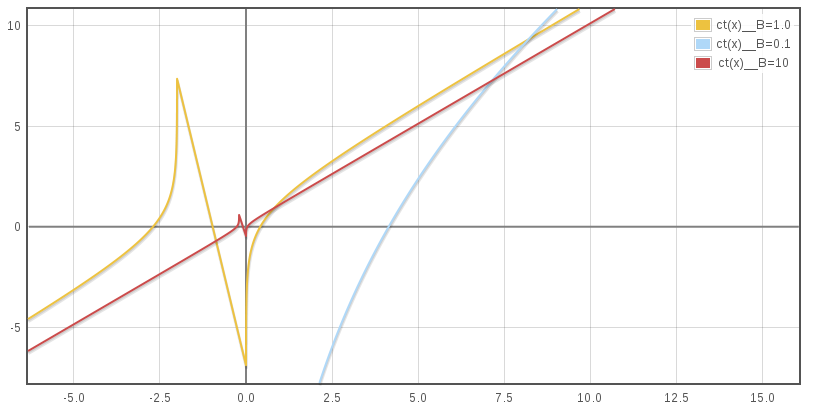
The curve asymptote when x tend towards +∞ for every values of B is x/c, which is the light speed corresponding line. This can also be deducted from (1.14) as if x/c is subtracted, the remaining terms tend to 1.348/B. The shift between curves summarize the ahead granted to a rocket with an other B after an infinite duration race started long in the past with both challengers swimming in a perfectly steady homogenous medium.
The motion of the ideal Bussard Ramjet is now algebraically solved in its proper frame as well as in the medium collected matter frame which can also be approximate as Earth rest frame.
The ideal Bussard Ramjet motion at low speed is according to (1.11), at best, exponential. Thus clearly this kind of device need an initial speed relative to the harvested medium. It is unlikely that this only propelling method is enough to cover all the travel.
However, at relativistic speed range its acceleration tend to B/2 when time goes to infinity, with respect to (1.8). To my opinion, it is the only theoretical device that exhibit a such capability. This ideal rocket should head the race, of theoretical, faster displacement speed.
Unfortunately any Bussard Ramjet practical achievement will experiment to any kind of loss leading to lesser capability.
[1] Galactic Matter and Interstellar Flight, Robert W. Bussard; Los Alamos Scientific Laboratory, University of California, Los Alamos, NM. Local mirror.
[2] Investigation of outer space rocket appliances, Konstantin Tsiolkovsky, 1903. Local mirror, See also Wiki, if one do not read russian.
[3] A note on relativistic rocketry, Acta Astronautica, Shawn Westmoreland, Volume 67, Issues 9-10, November-December 2010, pp. 1248 - 1251. Local mirror.
[4] Are Black Hole Starships Possible ?, Louis Crane, Shawn Westmoreland, 2009. Local mirror.
[5] Is Interstellar Travel Possible ?, Opik, E. J., Irish Astronomical Journal, vol. 6(8), p. 299. Local mirror.
[6] The equation of motion of an interstellar Bussard ramjet, Claude Semay and Bernard Silvestre-Brac, Eur. J. Phys. 26 (2005) 75–83, doi:10.1088/0143-0807/26/1/009. Local mirror.
[7] Short course in special relativity, M. Strovink, Spring 2006, University of California, Berkeley, Local mirror.
Mathematical image were produced with mimetex. Most of free web hosting do not provided arbitrary binary cgi-bin, formulas have been processed with this especially crafted script.
Reading the works quoted as reference has been a great help for this little work, particularly the Short course in special relativity of M. Strovink, as the article from Claude Semay and Bernard Silvestre-Brac [6].
I have also make a intensive use online calculation resources as WolframAlpha and Number Empire, especially for integration and graphics.
|
Here are some links for kids math education suggested by MathCamps.org:
|
|
Hosted by the courtesy of GitHub |
The stars ASAP


 Durée du voyage intersidéral  Résolutions de l'ONU en HTML  Bussard Ramjet 
 |
DWARF : dwarf2xml
 ELF : libelf examples  Code presentation : ctoohtml  |